Linear Optimization
Linear optimization (also called linear programming) is a method used to select optimal decisions. The key components of a linear optimization model are the decision variables, the objective, and the constraints.The decision variables in a linear optimization model represent the choices faced by the decision maker, and can take continuous values in a range. Examples are the number of gallons of crude oil to use to produce gasoline and the intensity of beams in radiation therapy. A linear optimization model is used to find the optimal values of these decision variables.
The objective in a linear optimization model is to maximize or minimize a linear function of the decision variables. Examples are to maximize total revenue, to minimize total cost, or to minimize the amount of radiation to healthy tissue. This is the ultimate goal of the linear optimization model.
The constraints in a linear optimization model are linear equations of the decision variables that must be satisfied by the solution of the model. They often represent feasibility problems in the model; if the constraints are not met, the solution will not work. Examples are to not produce more gasoline than the demand and to make sure the tumor gets enough radiation.
Integer Optimization
Integer optimization (also called integer programming) is similar to linear optimization, but the decision variables are constrained to take integer values (...,-3,-2,-1,0,1,2,3...) or binary values (0 or 1). Examples of integer decision variables are whether or not to invest in a stock, assigning nurses to shifts, the number of new machines to purchase in a factory, and the number of items to stock in a store. The objective and constraints are the same as in linear optimization: they must be linear functions of the decision variables.Optimization in LibreOffice and OpenOffice
Optimization models can be solved in many spreadsheet software programs, including LibreOffice and OpenOffice. Suppose we wish to solve the following very simple optimization model:This can be set up in a spreadsheet as follows:

The decision variable cells are highlighted in yellow. They are blank, since the model has not been solved yet. The objective cell is highlighted in blue. It is equal to 5 times the decision variable x (in cell B4), plus 3 times the decision variable y (in cell B5), plus 2 times the decision variable z (in cell B6). The constraints are highlighted in green. They are that (1) the sum of all decision variables must be less than or equal to 5, and that (2) z - x must be greater than or equal to zero. LHS here stands for "Left-hand side" of the constraint, and "RHS" stands for "Right-hand side" of the constraint.
To solve this model, you can select "Solver" from the "Tools" menu. A window will pop up that looks like the following:
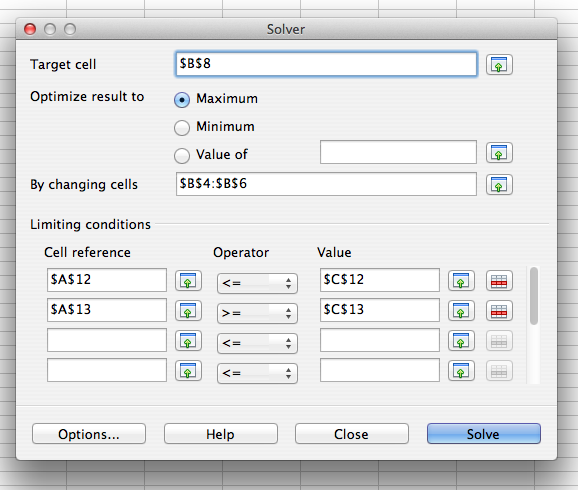
The values in "Target cell", "By changing cells", and "Limiting conditions" need to be filled in by you. The "Target cell" should be the objective cell, and the "By changing cells" should be the decision variable cells. Maximum or minimum should be selected based on whether the problem is a maximization problem or a minimization problem. In the "Limiting conditions" section, the "Cell reference" column should correspond to the cells in the LHS section of your model, the "Operator" column should correspond to the cells in the sign section of your model, and the "Value" column should correspond to the cells in the RHS section of your model.
If you select "Options..." you can check a box that says "Assume variables as non-negative". This makes it easy to make sure that all of the decision variables should have values greater than or equal to zero.
If you hit "Solve" and then "Keep Result", your spreadsheet should look like the following:
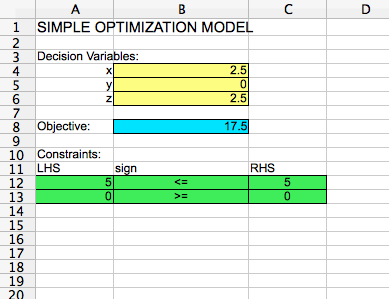
The optimal solution is x = 2.5, y = 0, and z = 2.5, with an optimal objective function value of 17.5.
If we would like to change the model to an integer optimization model by constraining the decision variables to integer values, we can do so by opening the solver again, and adding an integer restriction to the "Limiting conditions":
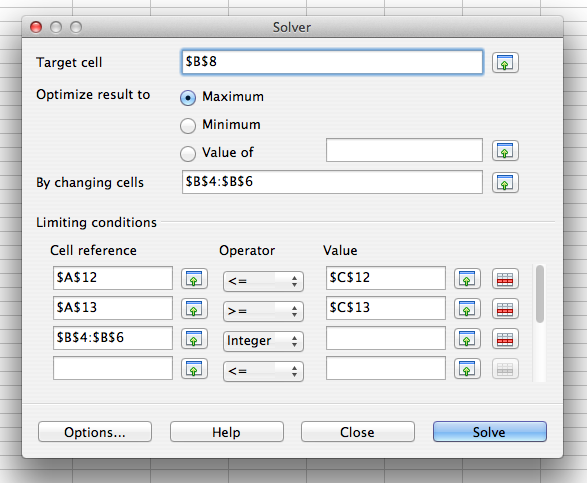
In the operator pull-down menu, you could alternatively select "Binary" to constrain the decision variables to take binary values. You don't need to put anything in the "Value" column for an integer or binary restriction. If you hit "Solve" and then "Keep Result", you get the optimal solution x = 2, y = 1, and z = 2, with an optimal objective function value of 17.